How to Solve Quadratics with Complex Numbers as the Solution
After you watch the video and know the material, click HERE for the quiz.
When you solve a quadratic equation with the quadratic formula and get a negative on the inside of the square root, what do you do? The short answer is that you use an imaginary number. For the longer, more helpful answer, check out this lesson!
Imaginary & Complex Numbers
By allowing ourselves to imagine that square roots of negative numbers actually exist, we are able to solve a lot of real-world problems. So, what does that actually look like? How would you go about solving a problem that has an imaginary solution? That's what this lesson is all about.
 |
You'll need to remember that imaginary numbers come about when we take the square root of a negative number, and complex numbers are when we combine a real number with an imaginary one using addition or subtraction. If this is a new concept for you, then you should check out the previous lesson that introduces these ideas, but if you already know this, we're ready to look at the example 'find the roots of y = 2x^2 - 5x + 7.'
Quadratics with Complex Solutions
When a problem asks you for the roots, it is the same thing as asking for the zeros or the x-intercepts. These are the points where y = 0, so we can substitute that value in to begin with.
 |
Given the fact that we're doing this example in the lesson all about complex number solutions, there's a good chance that's what this problem will have. But how could we know this if this problem wasn't in this context?
It's all going to come down to the discriminant. Given a quadratic equation in standard form (y = ax^2 + bx + c), the discriminant is b^2 - 4ac. If the discriminant is positive, you'll get two real answers. If it's equal to zero, you're only going to get one real answer. But if the discriminant is negative, that's when you get two complex solutions to your problem.
This is the case because of the way the quadratic formula works. If we begin to solve the example using the quadratic formula, as shown here, you might notice that the discriminant is the part of the formula that is inside the square root. Therefore, it makes sense that if that part is negative, we'll get an imaginary number there, making our answer a complex number.
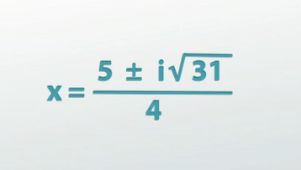 |
So, back to our example, if we substitute a, b and c into the formula and then begin to evaluate the expression, we'll find the discriminant will, sure enough, become negative. You'll see that we end up with the square root of -31, which is going to be an imaginary number. While this is what makes this problem new and different, the only special thing to do is to put an i in front of the square root to indicate it's imaginary, make everything else on the inside of the square root positive and then continue on just like we normally would. That's it! The i tells everyone that it is an imaginary number, but then we can move on and continue to solve the problem as normal.
As it turns out, there isn't even anything else to do with this problem; it's as simplified as it can be. Maybe if we could simplify the square root somehow, we might have a few more steps, but we can't do that, so we're good to go!
Polynomials with Complex Solutions
We can also solve polynomial problems with imaginary solutions that are bigger than quadratic equations. Take this example: Solve 0 = (x - 9)^2 * (x^2 + 9).
This isn't a quadratic equation anymore because there are two x^2s (here and here). We don't have any fancy formula for such problems like we do for quadratics, but because of the way this one is written, we can still solve it.
We're going to use the zero product property for this one. That's the property that says anytime you multiply two things together and get zero, one of the things you multiplied in the beginning must have been zero. In this problem, that means that either (x - 9)^2 or (x^2 + 9) must be zero. Now that we've split the equation up, we've got two smaller equations that we do know how to solve simply with inverse operations.
Getting the x by itself in this first one means undoing a power of 2 with a square root. The square root of zero is still just zero, so that leaves us here. Now, undoing -9 with +9 tells us that x = 9.
 |
Moving over to the other equation requires us to undo similar steps, just in a different order. The most outside thing here is the +9, so we have to undo that first. That leaves us with x^2 = -9, and then again we take the square root of both sides to get the x by itself. When we take the square root of a non-zero number, we need to include the positive and negative root, giving us two answers here.
We also have now taken the square root of a negative number, which means we have imaginary solutions as well! That means putting an i in front of the square root and continuing on like normal, just like before. This time we can go further because the square root of 9 is just 3. That makes our two other solutions here positive and negative 3i.
While this video is about how to solve problems with complex numbers, because the only thing you do is add an i and continue like normal, it's more a review of older solving skills. As long as you keep this in mind and don't think that complex numbers require you to do anything really radical, you should be good.
Lesson Summary
To review: the discriminant (b^2 - 4ac) will tell you whether you have real or complex solutions to a quadratic equation in standard form. When you need to take the square root of a negative number, just put an i in front of it, make the number on the inside positive and continue on like normal. You can solve higher-order polynomial problems using the zero product property, which says that when you multiply two things together and get zero, one of the things you started with must have been zero.