If the above player doesn't work, try this direct link.

Along with the change of base property, there are three other logarithmic properties that allow you to manipulate expressions to your advantage. Learn about the product rule, quotient rule and power rule here.

Logarithmic Properties

Once you've mastered evaluating logs, it's time to learn the tricks. Similar to how multiplication has the distributive property, logarithms have their own properties that will help us down the road when we are doing real-world problems. Because this video is about the nuts and bolts behind the fun stuff, it won't be the most exciting video ever, but I will try to make it as painless as possible.

The Product Property

The first property we'll learn is called the product property. Because logs are related to exponents, this is, actually, very similar to the exponent property called the product of powers property. It basically tells us that when we multiply two powers we get to add their exponents. As long as you remember that, we can come up with the product property for logs in the following way. Now, what I'm about to do is a mathematical proof of the product property. I'm not going to do this for all the properties in this video, but I do think it's good to see at least one of them so that you know that these things aren't just made up; they actually come from some math.

Now, all proofs need to start with some assumed information, so for this one we'll start by saying let log base b of x equal m and log base b of y equal n. That's two equations in logarithmic form, but if I change those same equations to exponential form, I get b^m = x and b^n = y. Therefore, if I multiply x and y, all I'm really doing is multiplying b^m * b^n, which then allows us to use the product of powers property of exponents, like we mentioned before, and add the exponents, so I get b^(m+n). This is still in expontential form, but if I change it back to logarithmic form, I'd have the log base b of x*y = m+n. But then going back to our original definition of what m and n were and substituting those in this equation, that gives us that the log base b of x*y equals the log base b of x plus the log base b of y. This is exactly what the product property of logarithms is.

The Quotient & Power Properties

If we do the exact same proof but with division instead of multiplication, we end up using the exponent property called the quotient of powers, and we get the quotient property of logarithms, which is that the log base b of x divided by y is equal to the log base b of x minus the log base b of y. Finally, if we use an exponent in our proof, we end up with the power property of logarithms, which tells us that the log base b of x^y is equal to y times log base b of x.

So, those are our three logarithmic properties - the product property, the quotient property and the power property. Having them written out formally, like we do here, is good if we want to be exact, but we can simplify the information from the properties by putting them into a table. What it really comes down to is this: what's going on inside the log, and what does the property tell us could be going on the outside? The product property says that if you see multiplying going on inside a log, you can change that to addition between logs on the outside. Similarly, the quotient property says that if we see division on the inside of the log, we can change it into subtraction between logs on the outside. And finally, the power property tells us that when you see an exponent on the inside of the log, we can change it into multiplication in front of the log.

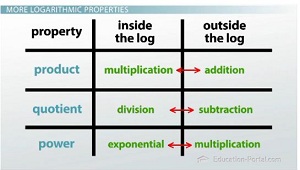Notice how I have little arrows drawn between each of the corresponding operations. That's because we can go back and forth using this property either way. For example, the quotient property says that if I see division on the inside, I can change it to subtraction on the outside, but if I see subtraction on the outside, I can go backwards and change it to division on the inside. We're going to be doing both.

We can now use this chart as a cheat-sheet for turning one complex log into a long chain of more simple logs or going the opposite direction and turning one long chain of simple logs into one complex one. For practice applying these properties to problems just like this, check out the next video, titled Practice Problems for Logarithmic Properties.

Lesson Summary

To review, besides the change of base property, there are three other logarithmic properties that allow us to manipulate logs. The product property says that when we take the log of two things being multiplied, we can split it up into two logs of those two things being added together. The quotient property says that when we take the log of a quotient, we can split it up into two logs that are being subtracted. The power property says that when we take the log of a power, we can bring down the exponent, bring it in front of the log and multiply.